Cliquer ici pour télécharger le fichier
L’objectif est de faire parler des données en calculant plusieurs indicateurs statistiques liés à cette série de données avec Excel.
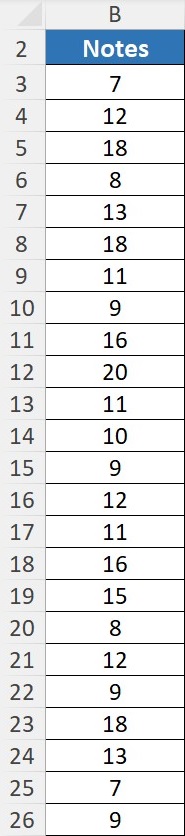
Exemple : On a une liste de notes obtenues par des étudiants et on souhaite calculer plusieurs indicateurs statistiques.
1) Le Mode
Le mode est la valeur la plus fréquente de la population d’une série de donnée étudiée.
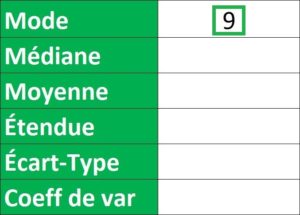
>> Mode = Formule MODE() => Il faut sélectionner toute la série de données.
= MODE(B3:B26)
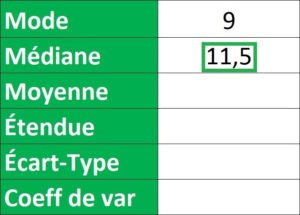
Résultat : La note de 9 est la note la plus fréquemment obtenue par les étudiants (elle apparaît 4 fois).
2) La Médiane
La médiane est la valeur qui permet de couper l’ensemble des valeurs en deux parties égales dans une série statistique ; C’est-à-dire qu’il y aura autant de valeurs supérieures ou égales à la médiane que de valeurs inférieures ou égales.
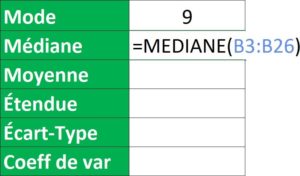
>> Médiane = Formule MEDIANE() => Il faut sélectionner toute la série de données.
= MEDIANE(B3:B26)
Résultat : Il y a autant de notes supérieures ou égales à 11,5 que de notes inférieures ou égales à 11,5.
Pour vérifier le résultat on va compter le nombre de valeurs situées des 2 côtés de la médiane avec la formule NB.SI :
= NB.SI( $B$3:$B$26 ; « >=11,5 » )
= NB.SI( $B$3:$B$26 ; « <=11,5 » )
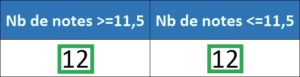
Résultat : Il y a 12 notes supérieures ou égales à la médiane et 12 qui sont inférieures ou égales à la médiane.
Évidemment la médiane n’est possible que dans le cas où il y a un nombre de valeurs paires (24 notes dans l’exemple) ; Si on rajoute un 25 valeurs dans l’exemple il y aura alors forcément plus de valeurs d’un côté de la médiane que de l’autre.
3) La Moyenne
La moyenne est égale au quotient de la somme de toutes les valeurs de cette série par l’effectif total ; Cela revient à additionner toutes les valeurs entre elles et diviser le résultat par le nombre de valeur.
- Moyenne = Formule MOYENNE() => Il faut sélectionner toute la série de données.
OU
- SOMME( liste de valeurs ) / NB( liste de valeurs ) => Pour calculer la moyenne des notes, il faut additionner toutes les notes avec la formule SOMME puis diviser le résultat par le nombre de notes avec la formule NB.
= MOYENNE(B3:B26)
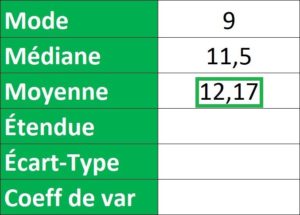
Résultat : 12,17 représente la moyenne des notes obtenues par les étudiants de cette classe.
4) L’Étendue
L’étendue représente la différence entre entre la plus grande et la plus petite valeur d’une série statistique.
>> Étendue = Différence entre le résultats des formules MAX() et MIN() => Il n’y a pas de formule Excel dédiée pour calculer directement l’étendue qui existe ; Il faut donc faire la différence entre le maximum et le minimum de la série statistique.
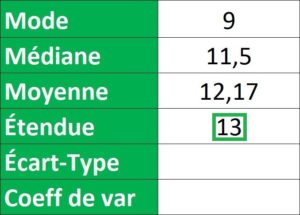
= MAX(B3:B26) – MIN(B3:B26) = 20 – 7 = 13
Résultat : Il y a un écart de 13 entre la note la plus élevée et la note la plus faible pour les notes obtenues par les étudiants de cette classe.
5) L’Écart-Type
L’écart-type est un indicateur de dispersion qui informe sur la manière dont se répartissent les données autour de la moyenne :
- Écart-type faible = Valeurs concentrées autour de la moyenne.
- Écart-type fort = Dispersion importante des valeurs autour de la moyenne.
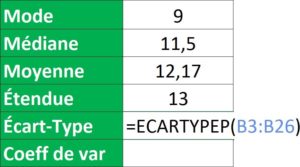
>> Écart-Type = Formule ECARTYPEP() : Cette formule ECARTTYPEP prend en compte l’hypothèse que les arguments représentent l’ensemble de la population => Il faut sélectionner toute la série de données.
Dans l’exemple les notes représentent bien l’ensemble de la population étudiée puisqu’on a la totalité des notes obtenues par les étudiants d’une classe (qui est la population étudiée).
Mais dans le cas où les données ne représentent qu’un échantillon de la population ; Imaginons qu’on est une population de 100 étudiants et qu’on ai uniquement les notes obtenues par 10 d’entre eux alors il serait alors plus judicieux d’utiliser la formule ECARTYPE (sans « P ») pour calculer l’écart-type de cette série de données.
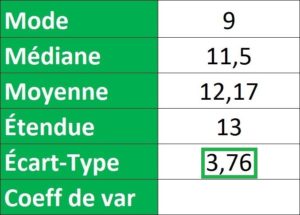
= ECARTYPEP(B3:B26)
Résultat : Pour pouvoir analyser plus facilement cet écart-type il faut maintenant calculer le coefficient de variation.
6) Le coefficient de variation
Le coefficient de variation est une mesure relative de la dispersion des données autour de la moyenne : Il est égal au ratio de l’écart-type par rapport à la moyenne. Plus la valeur du coefficient de variation est élevée, plus la dispersion autour de la moyenne est grande.
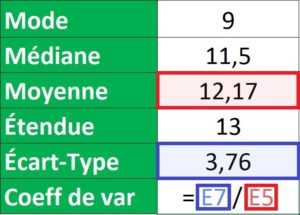
>> Coefficient de Variation = Ratio entre les résultats des formules ECARTTYPEP() et MOYENNE().
= E7 (Écart-Type) / E5 (Moyenne)
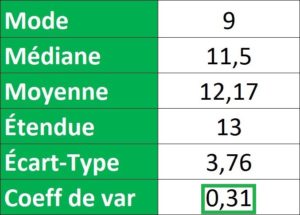
Résultat : Le coefficient de variation est de 0,31 = C’est-à-dire que l’écart-type représente un peu moins d’un tiers de la moyenne ; On considère qu’un écart-type commence à être élevé lorsqu’il représente la moitié de la moyenne, il est donc relativement faible dans l’exemple. Si on observe les notes obtenues on constate qu’elles sont plutôt concentrées autour de la moyenne.
=> Voir aussi comment Classer des valeurs